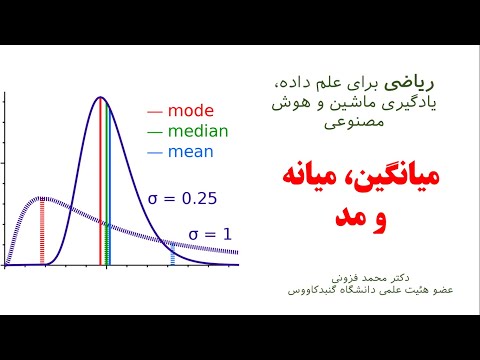
میانگین در مقابل حالت متوسط در مقابل حالت
میانگین، میانه و حالت معیارهای اولیه گرایش مرکزی هستند که در آمار توصیفی استفاده می شوند. آنها کاملاً با یکدیگر متفاوت هستند و مواردی که در آنها برای خلاصه کردن داده ها استفاده می شود نیز متفاوت است.
میانگین
میانگین حسابی مجموع مقادیر داده تقسیم بر تعداد مقادیر داده است، یعنی
[latex]\bar{x}=\frac{1}{n}\sum_{i=1}^{n}x_{i}=\frac{x_{1}+x_{2} +x_{3}+…+x_{n}}{n}[/latex]
اگر داده ها از فضای نمونه باشد، میانگین نمونه ([latex]\bar{x} [/latex]) نامیده می شود که یک آمار توصیفی از نمونه است.اگرچه رایجترین معیار توصیفی مورد استفاده برای یک نمونه است، اما آمار محکمی نیست. به نقاط دورافتاده و نوسانات بسیار حساس است.
برای مثال، متوسط درآمد شهروندان یک شهر خاص را در نظر بگیرید. از آنجایی که تمام مقادیر داده ها جمع و سپس تقسیم می شوند، درآمد یک فرد بسیار ثروتمند به طور قابل توجهی بر میانگین تأثیر می گذارد. بنابراین، مقادیر میانگین همیشه نمایش خوبی از داده ها نیستند.
همچنین در مورد سیگنال متناوب، جریان عبوری از یک عنصر بطور دوره ای از جهت مثبت به جهت منفی و بالعکس تغییر می کند. اگر میانگین جریان عبوری از عنصر را در یک دوره واحد در نظر بگیریم، 0 می دهد، به این معنی که هیچ جریانی از عنصر عبور نکرده است، که بدیهی است که درست نیست. بنابراین، در این مورد نیز میانگین حسابی معیار خوبی نیست.
میانگین حسابی زمانی که داده ها به طور مساوی توزیع شده اند، شاخص خوبی است.برای توزیع نرمال، میانگین برابر با مد و میانه است. همچنین هنگام در نظر گرفتن ریشه میانگین مربعات خطا، کمترین باقیمانده را دارد. بنابراین، بهترین معیار توصیفی زمانی که لازم است یک مجموعه داده را با یک عدد نشان دهیم.
میانگین
مقادیر نقطه داده میانی پس از مرتب کردن تمام مقادیر داده ها به ترتیب صعودی به عنوان میانه مجموعه داده تعریف می شود. میانه چارک دوم، دهک 5 و صدک 50 است.
• اگر تعداد مشاهدات (نقاط داده) فرد باشد، میانه مشاهده دقیقاً در وسط فهرست مرتب شده است.
• اگر تعداد مشاهدات (نقاط داده) زوج باشد، میانه میانگین دو مشاهدات میانی در لیست مرتب شده است.
Median مشاهدات را به دو گروه تقسیم می کند. یعنی یک گروه (50%) از مقادیر بالاتر و یک گروه (50%) از مقادیر کمتر از میانه. میانه ها به طور خاص در توزیع های اریب استفاده می شوند و داده ها را نسبتاً بهتر از میانگین حسابی نشان می دهند.
حالت
Mode بیشترین تعداد در مجموعه ای از مشاهدات است. حالت یک مجموعه داده با یافتن فراوانی هر عنصر در مجموعه محاسبه می شود.
• اگر هیچ مقداری بیش از یک بار رخ ندهد، مجموعه داده هیچ حالتی ندارد.
• در غیر این صورت، هر مقداری که با بیشترین فرکانس رخ می دهد، حالتی از مجموعه داده است.
بیش از 1 حالت می تواند در یک مجموعه وجود داشته باشد. بنابراین، حالت یک آمار منحصر به فرد از یک مجموعه داده نیست. در توزیع یکنواخت، یک حالت وجود دارد. حالت توزیع احتمال گسسته نقطه ای است که تابع جرم احتمال به بالاترین نقطه خود می رسد. با برداشت از تفاسیر بالا، میتوان گفت که ماکزیممهای جهانی حالت هستند.
کاربرد هر سه معیار را برای مجموعه داده زیر در نظر بگیرید.
داده: {1، 1، 2، 3، 5، 5، 5، 5، 6، 6، 8، 8، 9، 9، 9، 9، 9، 10، 10، 10، 14، 14، 15، 15، 15}
میانگین=(1+ 1+ 2+ 3+ 5+ 5+ 5+ 5+ 6+ 6+ 8+ 8+ 9+ 9+ 9+ 9+ 10+ 10+ 10+ 14+ 14+ 15+ 15+ 15) / 25=8.12
میانگین=9 (سیزدهمین عنصر)
حالت=9 (فرکانس 9=5)
تفاوت بین میانگین، میانه و حالت چیست؟
• میانگین حسابی مجموع مقادیر (مشاهدات) تقسیم بر تعداد مشاهدات است. این یک آمار قوی نیست و به شدت به ماهیت توزیع نرمال در توزیع در نظر گرفته شده وابسته است. یک نقطه پرت ممکن است باعث تغییر قابل توجهی در میانگین دادن مقادیر نسبتا گمراه کننده شود. این مفهوم را می توان به میانگین هندسی، میانگین هارمونیک، میانگین وزنی و غیره تعمیم داد.
• میانه مقادیر میانی مجموعه مشاهدات است و نسبتاً کمتر تحت تأثیر عوامل پرت قرار می گیرد. ممکن است تخمین خوبی به عنوان آمار خلاصه در موارد بسیار ناهنجار ارائه دهد.
• حالت رایج ترین مقادیر مشاهده در مجموعه داده است. اگر توزیع دارای انحراف مثبت باشد، حالت به سمت میانه قرار می گیرد و اگر دارای انحراف منفی باشد، حالت به سمت میانه قرار می گیرد.
• اگر دارای انحراف مثبت باشد، میانگین درست به میانه است. اگر دارای انحراف منفی باشد، میانگین در سمت چپ میانه است.
• در توزیع نرمال، هر سه، میانگین، حالت و میانه برابر هستند.